I forrige uke holdt jeg en ekte forelsning, for første gang på en stund. Han som vanligvis foreleser kvantemekanikk for fysikkstudentene er bortreist, så han spurte om jeg kunne være vikar og gi dem en introduksjon til Python, Eulers metode og Monte Carlo-integrasjon, og ellers legge opp forelesningen slik jeg følte for. Jeg takket naturligvis ja, og nå er jeg nettopp ferdig. Det er ikke helt greit å si hvordan det gikk, studentene nå til dags gir ikke så veldig mye feedback underveis, men jeg fikk applaus til slutt så jeg tror jeg sier meg fornøyd.
Monte Carlo-simuleringer er et uttrykk enkelte liger å slenge rundt seg. Hva det betyr kommer helt an på hvem du snakker med, da mange bruker dette om spesifikke varianter, men helt generelt er Monte Carlo-simuleringer en eller annen beregning som bruker tilfeldige tall. Dette kan for eksempel være nyttig når man ser på tilfeldige prosesser, hvor man ønsker å kjøre en simulering mange ganger og ta et eller annen gjennomsnitt, men det kan også brukes til ting som ikke nødvendigvis har noe med tilfeldigheter å gjøre. Et eksempel er Monte Carlo-integrasjon.
Integrasjon går, sånn omtrent, ut på å finne arealet under en kurve. Dette kan man ofte gjøre med papir og blyant og ren matematikk, men av og til er det enklere, eller til og med nødvendig, å ty til numeriske metoder. La oss ta et eksempel:
Sett at vi ønsker å finne arealet under kurven gitt av \(f(x)=x^2\), fra 0 til 1, som er det samme som å regne ut
$$
\int_0^1 x^2 \;\mathrm{d}x.
$$
Dette integralet er ganske rett frem å regne ut analytisk, men la oss gå for en numerisk løsning likevel. Den enkleste og mest intuitive måten å beregne et integral numerisk er antagelig det som kalles en Riemann-sum. Det går ut på å dele opp området man ser på, i dette tilfellet fra 0 til 1, i mindre biter, og regne ut verdien av funksjonen i midtpunktet av hver av disse bitene. For hvert sub-intervall regner man så ut funksjonverdien ganger bredden av sub-intervallet, som tilsvarer å finne arealet av et rektangel. Legg sammen alle disse arealene, og vips har man en tilnærming til det totale arealet under kurven.
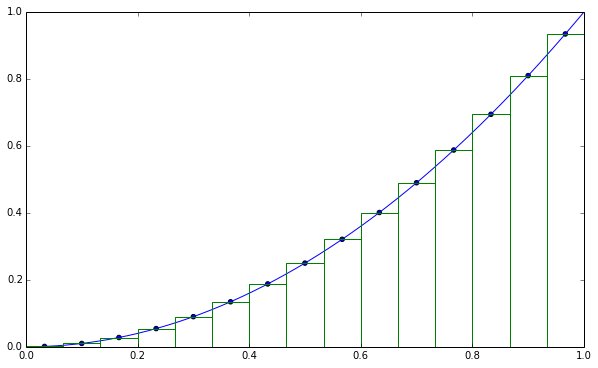
Riemann-sum
Den enkleste varianten av Monte Carlo-integrasjon går mye på samme måte. Den eneste forskjellen er at man velger midtpunktene sine tilfeldig, i stedet for å fordele dem jevnt. Man regner fortsatt ut funksjonsverdien i et antall punkter, og man tilnærmer fortsatt arealet under kurven med en sum av arealer av rektangler.
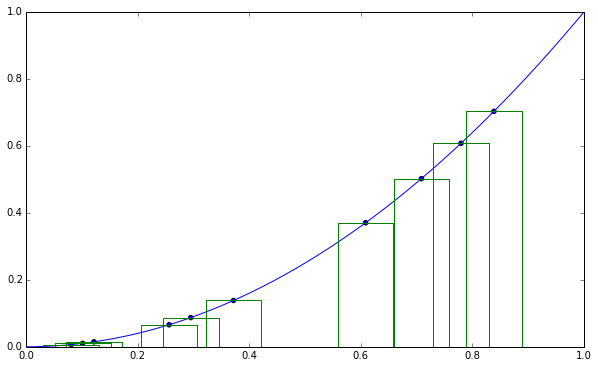
Monte Carlo-integrasjon
Første gangen jeg hørte om dette tenkte jeg at dette høres ut som tull. Greit nok at Hvis du bruker mange nok punkter vil Monte Carlo-integrasjon gi en god tilnærming til svaret, men vil man ikke alltid få et minst like bra svar ved å ta Riemann-summen? Det viser seg imidlertid at dette ikke alltid er tilfelle, og det er ganske greit å konstruere et eksempel der Monte Carlo-integrasjon funker bedre. La oss for eksempel ta en kikk på integralet
$$
\int_0^1 \sin^2 (10\pi x) \;\mathrm{d}x.
$$
Observante lesere vil umiddelbart se hva som skjer om vi prøver å beregne dette integralet ved en Riemann-sum med litt uheldig plassering av punkter:
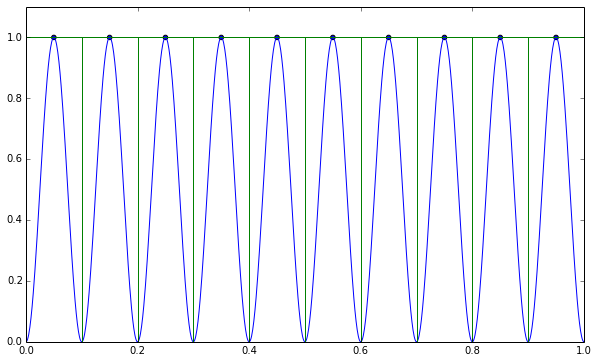
Riemann-sum
Det som har skjedd her er at vi har forsøkt å integrere en periodisk varierende funksjon ved å se kun på punkter som «tilfeldigvis» ligger i samme avstand som toppene til funksjonen. Går vi derimot for Monte Carlo-integrasjon er det ganske god sannsynlighet for at vi får et bedre gjennomsnitt av funksjonen ved å sample litt her og litt der, og resultatet blir typisk mye bedre.
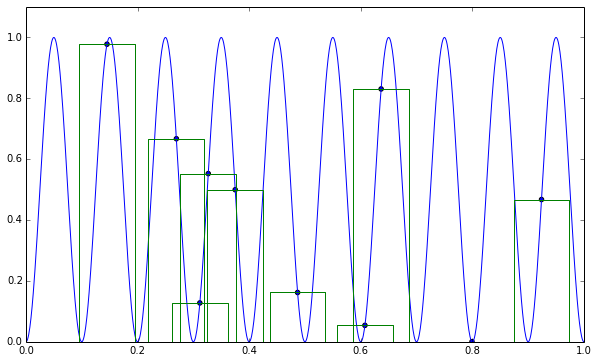
Monte Carlo-integrasjon
Dette eksempelet er naturligvis konstruert for å vise hvor galt det i verste fall kan gå, men moralen gjelder mer generelt. I en del tilfeller, for eksempel når man har med raskt varierende funksjoner å gjøre, kan Monte Carlo-integrasjon gi bedre resultater enn metoder basert på jevnt fordelte punkter.





Comments