Jeg skrev ved en tidligere anledning om hvordan det er fort gjort å brenne seg hvis man ikke tenker over konsekvensene av at
datamaskiner lagrer tall med endelig presisjon. I dag tenkte jeg å utdype litt, med et noe mer realistisk eksempel.
Av ulike grunner prøver jeg i simuleringskoden jeg har skrevet i løpet av doktorgraden å regne ut en litt småsuspekt rekkeutvikling. Grovt sagt regner jeg ut en eksponentialfunksjon ved hjelp av den kjente rekken
Denne rekken, som er en av måtene man kan definere eksponentialfunksjonen, er alltid konvergent. Den vil altså alltid gi riktig resultat, uansett hva argumentet
x er. Problemet, som jeg ikke tenkte helt over til å begynne med, er at denne rekkeutviklingen funker spekakulært dårlig hvis man prøver å gjøre den for moderat store negative tall. Jeg fikk derfor en litt utrivelig overraskelse her for en tid tilbake, da jeg prøvde å simulere et system som hadde litt større verdier for forskjellige parametere enn de jeg hadde sett på tidligere, og resultatet bare så ut som tilfeldige enorme tall.
For å ta et eksempel kan vi kikke på hva som skjer hvis vi prøver å regne ut
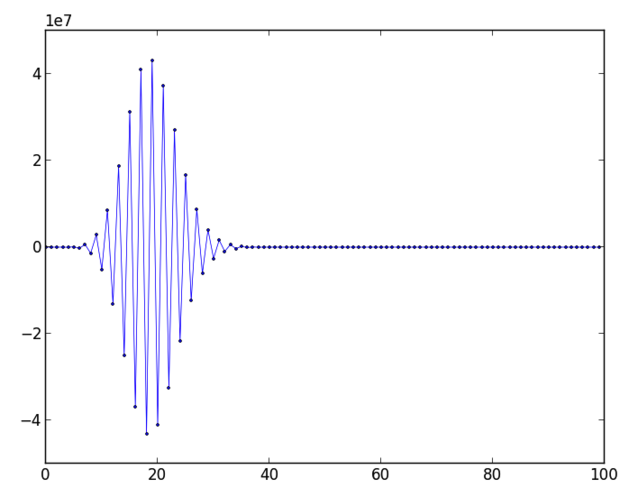
e-20. Jeg har gjort rekkeutviklingen, og laget en figur som viser de 100 første leddene:
Det er vanskelig å se nøyaktig hva de ulike verdiene er, men essensen jeg prøver å få frem med dette plottet er at leddene i serien er vekselvis positive og negative, og varierer veldig mye i størrelsesorden. Serien begynner på -20, vokser til 4.3 x 10
7 og når vi kommer til ledd nummer hundre har den sunket til 1.4 x 10
-28. Svaret skal bli 2.06 x 10
-9, så de siste leddene har nok ikke så mye å si, men de største leddene har derimot en hel del å si. Som vi husker har man ca 17 siffer å støtte seg på når man jobber i dobbel presisjon, og vi ser at det jeg prøver å gjøre her er å ta differansen mellom digre tall, for så å forvente å få et fornuftig resultat som er 17 størrelsesordener mindre. Åpenbart en dårlig idé.
Løsningen her er naturligvis å bruke høyere presisjon. Det er imidlertid ikke fullt så rett frem som man skulle tro. Det er selvfølgelig ikke noe problem med nok minne, jeg trenger bare å huske noen få tall av gangen, og et par hundre siffer hadde holdt i massevis, så det er ikke noe stress. Problemet er at prosessorer nå om dagen er bygget med 64-bits registere. Jeg er ikke noen guru på prossesordesign, akkurat, men essensen, slik jeg har forstått det, er at når du ganger sammen to tall i dobbel presisjon blir de lastet inn i to registere i prosessoren, og så kjører man dem gjennom en multiplikasjonsprosess som i stor grad er implementert i hardware. Hvis man derimot ønsker å bruke kvadruppel presisjon, der hvert tall tar 128 bit, må man lagre tallene fordelt over flere registere og bruke software for å sy sammen resultatet til slutt, og vips går det 50 ganger tregere enn dobbel presisjon.
Moralen er altså at man ikke skal kimse av hardware, og at det er bare å glede seg til det kommer prosessorer med 128-bits registere. Skjønt, jeg tror ikke akkurat det er noen skrikende etterspørsel, så det kan fort bli noen år til. Uten at jeg er helt sikker på hvorfor later det til å være en viss sammenheng mellom størrelsen på prosessorregistere for flyttall og størrelse på adresserommet man bruker til minneadressering, og med 64-bits adresserom kan man omtrent adressere hvert eneste atom i universet, så det ligger ikke an til å bli noe problem med det første.

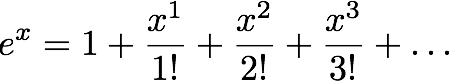
Comments