2.7182818284590452353602874713526...
I går ettermiddag var en slektning av Trond innom oss, og han stilte et interessant spørsmål, nemlig hvor kommer egentlig tallet
e fra. Det dukker jo opp over alt når man prøver å regne på ting, så det må jo være noe spesielt med det. Jeg ble kanskje litt overrumplet, og svarte kanskje litt kort, så jeg skal utdype i denne artikkelen.
For mange Herrens år siden var det en fyr som het Jacob Bernoulli, som satt og tenkte på dette med rente. Sett at du setter inn 1 krone, på en konto som gir 100% rente pr. år. Hvis man legger til renten en gang på slutten av året, vil du etter et år ha 2 kroner på bok. Hvis derimot renten blir beregnet to ganger i året, vil du først få lagt til 50% etter et halvt år, som vil gi deg totalt 1,50, og deretter vil du få ytterligere 50% etter et helt år. Da vil du altså ha 2,25 kroner. Det Bernoulli oppdaget, er at når du beregner renten stadig oftere, vil beløpet du ender opp med nærme seg en grense, som viser seg å være
e=2,718281828...
På videregående lærte vi et generelt uttrykk for å beregne rente etter et antall utdelinger. Det var noe slikt som dette:
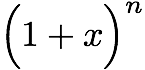
der
x er renten og
n er antall ganger den deles ut. Hvis vi setter inn at vi skal dele ut renten
n ganger i året, må vi endre renten til å være 1/
n, og vi må opphøye i
n. Hvis vi så tar grensen der
n går mot uendelig, har vi funnet et uttrykk for
e.
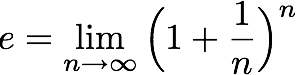
Det er imidlertid ikke et spesielt praktisk uttrykk, og vi skal se at det finnes andre måter å beregne
e. Du kan imidlertid teste dette uttrykket selv på en kalkulator. Hvis du begynner med
n = 2, og prøver noen få tall oppover mot 10000, vil du se at du nærmer deg en grense.
e fremkommer imidlertid andre steder også. Det mest kjente eksempelet er kanskje når vi ser på derivasjon. Som vi sikkert husker, den deriverte av en funksjon gir oss stigningstallet til funksjonen, altså hvor bratt kurven stiger eller synker.

Det som er spesielt med
e i denne sammenhengen, er at funksjonen
e opphøyd i
x er sitt eget stigningstall, altså
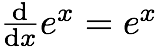
Og det er nettopp denne egenskapen som gjør at det er veldig hendig å bruke
e til alt mulig rart.
e er forøvrig et eksempel på det vi kaller et irrasjonalt tall. Det vil si at det ikke kan skrives som en brøk av to hele tall, og er det samme som at uansett hvor mange desimaler av
e du skriver ut, vil du aldri finne et repeterende mønster.
Så hvordan beregner man så
e? Det finnes flere metoder, som alle er en eller annen form for uendelig rekke, der man får stadig mer nøyaktige verdier jo flere operasjoner man gjør. Det enkleste eksempelet er kanskje
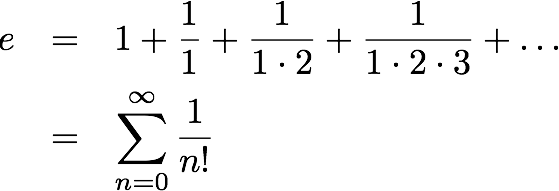
Så hvor mange siffer av
e kjenner vi egentlig? I følge wikipedia, hvor jeg forresten også har stjålet historien om Bernoulli, har to fyrer ved navn Shigeru Kondo og Steve Pagliarulo beregnet de første hundre milliarder siffer av
e. Det blir altså en txt-fil på 100 gigabyte, og er antagelig mest for spesielt interesserte. For oss mer vanlige holder det nok lenge med den første millionen, som du kan finne
her.
-Tor Nordam

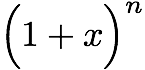
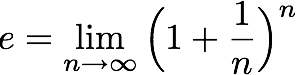

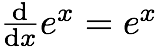
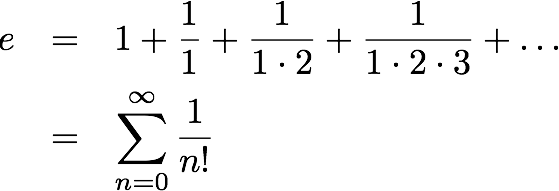
Comments